Maze Problem BNUOJ 1055

题目描述

Time Limit: 1000ms		
Memory Limit: 65535KB

走迷宫是很有趣的一种游戏,能够锻炼人的记忆力和思维.
现在,HK被困在一个迷宫里面了,请你帮助他计算一下有多少种不同的走法,能够让他走出迷宫.
这个迷宫很奇怪,HK只能够沿着向上或者向右的方向走,不能回头.

迷宫使用一个N*M的矩阵来描述,矩阵中用'.'代表空格可以通行,
用'*'代表障碍物,用'S'代表出发点,用'T'代表出口.例如下面的一个矩阵就描述了一个8*8的迷宫

.....T..
..*****.
......*.
*.***.*.
......*.
.****.*.
S..*....
........

Input

每个输入文件只包含一组输入数据.
每组数据第一行是两个正整数N和M(N,M<=100).
接着是一个N*M的矩阵.

Output

输出HK能够选用的不同方法数(由于结果可能很大,输出模1908的余数即可).
8 8
.....T..
..*****.
......*.
*.***.*.
......*.
.****.*.
S..*....
........

Sample Output
1

问题分析

看到这个题我的第一反应是用dfs,从起点开始，一次检索两个方向上的可能性， 如果符合题意，则继续深入递归，直至到达终点，让count++并返回，

继续递归。

于是我写了一个dfs的程序，本地测试了几组数据，都是正常产出。

我把代码交到oj，结果很意外：Time Limit Exceed。

但是仔细想想，就不难发现，因为在递归调用的时候，重复计算了太多问题。

因为之前某种方法走到某一点后的状态，从这点到终点的方法数会在之后某种方法中途到底此点后再次调用dfs递归计算，这简直就是扯淡。

重复计算？想到了什么？

对，就是dp！

动态规划有两种基本结构：

• 带备忘的自顶向下的递归 就是把之前的算过的一些dfs值储存在一个数组里，把重复的递归调用转化为数组数据的直接访问。

• 自底向上的动态规划 ​ 就是把问题分成一系列子问题之后，找清楚各个子问题之间的相互依赖关系，即子问题的子问题，子子问题，然后从最小规模的子问题开始计算，自底向上，保证只有当某个问题的所有依赖子问题都计算完成后，才计算这个问题。

  这两种算法时间界相近，第二种系数更小些。）

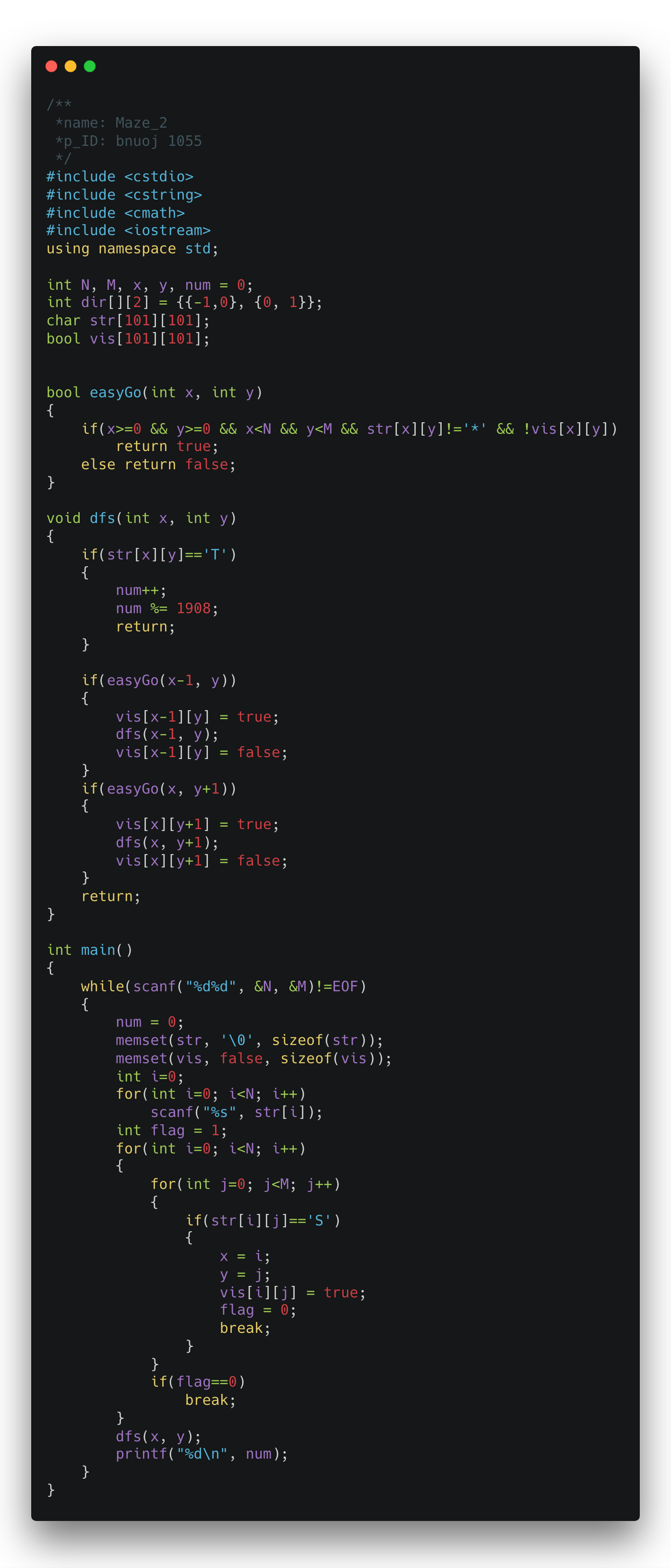
把原来的dfs也附上，方便反省。。。

​