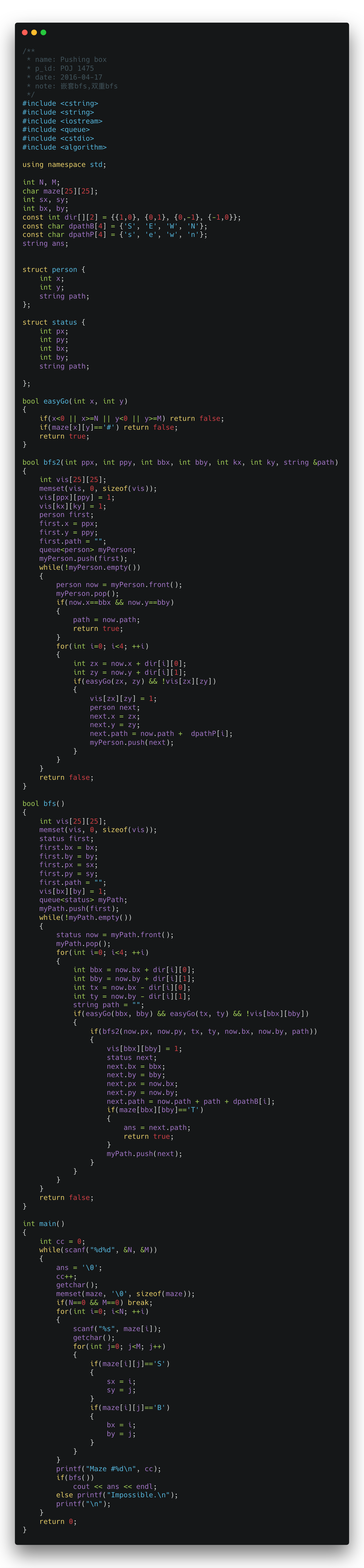
POJ 1475 推箱子
题目描述
Name: Pushing Boxes
P_ID: POJ 1475
description:
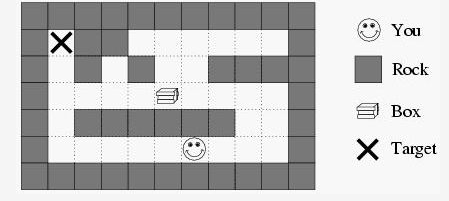
Imagine you are standing inside a two-dimensional maze composed of square cells which may or may not be filled with rock. You can move north, south, east or west one cell at a step. These moves are called walks.
One of the empty cells contains a box which can be moved to an adjacent free cell by standing next to the box and then moving in the direction of the box. Such a move is called a push. The box cannot be moved in any other way than by pushing, which means that if you push it into a corner you can never get it out of the corner again.
One of the empty cells is marked as the target cell. Your job is to bring the box to the target cell by a sequence of walks and pushes. As the box is very heavy, you would like to minimize the number of pushes. Can you write a program that will work out the best such sequence?
Input:
The input contains the descriptions of several mazes. Each maze description starts with a line containing two integers r and c (both <= 20) representing the number of rows and columns of the maze.
Following this are r lines each containing c characters. Each character describes one cell of the maze. A cell full of rock is indicated by a `#' and an empty cell is represented by a `.'. Your starting position is symbolized by `S', the starting position of the box by `B' and the target cell by `T'.
Input is terminated by two zeroes for r and c.
Output:
For each maze in the input, first print the number of the maze, as shown in the sample output. Then, if it is impossible to bring the box to the target cell, print ``Impossible.''.
Otherwise, output a sequence that minimizes the number of pushes. If there is more than one such sequence, choose the one that minimizes the number of total moves (walks and pushes). If there is still more than one such sequence, any one is acceptable.
Print the sequence as a string of the characters N, S, E, W, n, s, e and w where uppercase letters stand for pushes, lowercase letters stand for walks and the different letters stand for the directions north, south, east and west.
Output a single blank line after each test case.
Sample Input:
1 7
SB....T
1 7
SB..#.T
7 11
###########
#T##......#
#.#.#..####
#....B....#
#.######..#
#.....S...#
###########
8 4
....
.##.
.#..
.#..
.#.B
.##S
....
###T
0 0
Sample Output:
Maze #1
EEEEE
Maze #2
Impossible.
Maze #3
eennwwWWWWeeeeeesswwwwwwwnNN
Maze #4
swwwnnnnnneeesssSSS
思路
刚看完这道题,第一反应这玩意儿不是小时候玩的那个推箱子吗?嗯,就是那个推箱子。 接下来我主要想到了这些东西:
-
先找box的最短路,也就是先对box到target进行bfs
-
再找从人到箱子的最短路,也就是对人P到box进行bfs
很容易发现这种思路有一个问题,就是即使已经找到了一个从箱子到目标T的最短路径,也找到了从人到箱子的初始位置的最短路,也不一定能保证就能得到题目的解。因为有可能某一个位置是无法推的(角落)。 所以我的第一反应是在加一个角落判断函数,即如果在箱子走向target的过程中出现了角落位置,则不走。也就是说这样就保证了凡事箱子走出来的路径一定是可以被人推着走的。
但是事实是这个解法似乎不太符合题意。因为在箱子走的路径的中间过程,其实也是可能人需要走一些多于的路(不仅仅是推箱子)以到达合适的推箱子部位,这不利于输出路径。
我在status找到一个AC代码,研究了他的代码以后发现他的思路其实是一个嵌套bfs(其实在acm里这个应该是很常见的。。。小白了一把。。。)
- 优先对箱子进行bfs,每移动一次箱子,就对人也进行一次bfs,这次bfs主要是为了找到人从当前路径走到推动箱子到下一步所需的位置的最短路径。这个位置的控制是这样的: 将人的目标移动距离设置为箱子相对于下一步移动的相反位置一个cell格子内。(这是正常的推箱子方向),这一步其实就保证了绝对不会出现进入墙角的现象,因为如果某一次箱子的移动导致了进入墙角,那么在之后人的bfs的时候,将因为无法到达箱子再下一步的移动位置相反位置的cell而返回false,进而在箱子的bfs中导致此次移动无效,队列开始下一个位置的循环。 也就是采用:
int bbx = now.bx + dir[i][0];//box_x
int bby = now.by + dir[i][1];//box_y
int tx = now.bx - dir[i][0];//target_person_x
int ty = now.by - dir[i][1];//target_person_y
- 然后对人进行bfs即可
参考代码: